Power Spectrum Computation#
Introduction#
The main entry point to the power spectrum module is the calc_power() function, which takes a set of points, deposits them onto a mesh (optionally with interlacing), computes the mode powers through an FFT, and then computes bandpowers and multipoles. This notebook is a quick demonstration of that function, with a similarly quick sanity check against nbodykit.
Example#
import numpy as np
import matplotlib.pyplot as plt
from abacusnbody.analysis.power_spectrum import calc_power
Load the data:
power_test_data = dict(**np.load("../../../tests/data_power/test_pos.npz"))
Lbox = 1000.
pos = power_test_data['pos']
Specifications of the power spectrum computation. The only required args are pos and Lbox.
interlaced = True
compensated = True
paste = 'TSC'
nmesh = 72
nbins_mu = 4
logk = False
k_hMpc_max = np.pi*nmesh/Lbox + 1.e-6
nbins_k = nmesh//2
poles = [0, 2, 4]
Compute the power spectrum, including bandpowers and multipoles:
power = calc_power(pos, Lbox, nbins_k, nbins_mu, k_hMpc_max, logk, \
paste, nmesh, compensated, interlaced, poles=poles)
The result is an Astropy Table. The shape of the k_avg, power, etc, columns is (nbins_k,nbins_mu). The poles column is shape (nbins_k,len(poles)).
power
| k_min | k_max | k_mid | k_avg | power | N_mode | poles | N_mode_poles | mu_min | mu_max | mu_mid |
|---|---|---|---|---|---|---|---|---|---|---|
| float64 | float64 | float64 | float32[4] | float32[4] | int64[4] | float32[3] | int64 | float64[4] | float64[4] | float64[4] |
| 0.0 | 0.006283213084957364 | 0.003141606542478682 | 0.005026548 .. 0.0062831854 | 7568.9023 .. 6049.0254 | 5 .. 2 | 7134.6523 .. 33801.098 | 7 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.006283213084957364 | 0.012566426169914728 | 0.009424819627436047 | 0.010726068 .. 0.012566371 | 2942.2803 .. 49420.074 | 8 .. 2 | 12721.525 .. 8581.41 | 26 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.012566426169914728 | 0.018849639254872094 | 0.015708032712393412 | 0.016180087 .. 0.01517894 | 9128.091 .. 26119.805 | 16 .. 18 | 17876.928 .. -4302.0957 | 90 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.018849639254872094 | 0.025132852339829457 | 0.021991245797350775 | 0.022035956 .. 0.022221854 | 9138.691 .. 20882.14 | 20 .. 42 | 16421.23 .. -2728.3147 | 134 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.025132852339829457 | 0.031416065424786824 | 0.02827445888230814 | 0.0278653 .. 0.02873107 | 9497.041 .. 21889.508 | 80 .. 58 | 14460.294 .. 1471.5734 | 258 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.031416065424786824 | 0.03769927850974419 | 0.0345576719672655 | 0.03427213 .. 0.0344824 | 8653.626 .. 17725.803 | 112 .. 90 | 13018.891 .. -5607.4976 | 410 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.03769927850974419 | 0.04398249159470155 | 0.04084088505222287 | 0.04038116 .. 0.04089897 | 8631.141 .. 15932.965 | 108 .. 138 | 11582.084 .. 430.21402 | 494 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.04398249159470155 | 0.050265704679658914 | 0.04712409813718023 | 0.046560723 .. 0.04736551 | 8191.2383 .. 14180.858 | 144 .. 178 | 10757.994 .. -2565.6487 | 690 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.050265704679658914 | 0.05654891776461628 | 0.0534073112221376 | 0.053127706 .. 0.053584747 | 8125.8447 .. 13207.899 | 280 .. 226 | 9751.573 .. -19.154434 | 962 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.05654891776461628 | 0.06283213084957365 | 0.05969052430709496 | 0.05940248 .. 0.05961299 | 7919.7124 .. 12426.76 | 280 .. 274 | 9381.509 .. 696.6776 | 1098 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 0.16336354020889146 | 0.16964675329384885 | 0.16650514675137015 | 0.16650459 .. 0.16650878 | 3508.4248 .. 4512.569 | 2208 .. 2234 | 3929.0388 .. -230.04236 | 8994 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.16964675329384885 | 0.1759299663788062 | 0.1727883598363275 | 0.17277633 .. 0.17290868 | 3562.9634 .. 4224.724 | 2212 .. 2418 | 3855.428 .. 27.31195 | 9446 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.1759299663788062 | 0.18221317946376356 | 0.1790715729212849 | 0.17895347 .. 0.17909919 | 3525.7412 .. 4377.7456 | 2600 .. 2458 | 3806.5596 .. 139.75587 | 9978 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.18221317946376356 | 0.18849639254872091 | 0.18535478600624222 | 0.185251 .. 0.1852861 | 3623.513 .. 4494.107 | 2864 .. 2762 | 3875.3442 .. 257.82697 | 11138 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.18849639254872091 | 0.1947796056336783 | 0.1916379990911996 | 0.19156447 .. 0.19152866 | 3384.806 .. 4229.843 | 2836 .. 2890 | 3696.4075 .. 195.4255 | 11406 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.1947796056336783 | 0.20106281871863566 | 0.197921212176157 | 0.19781813 .. 0.19785866 | 3382.7285 .. 4218.5186 | 2960 .. 3186 | 3763.8347 .. -332.63657 | 12578 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.20106281871863566 | 0.207346031803593 | 0.20420442526111432 | 0.20413305 .. 0.20423785 | 3378.4102 .. 4038.1118 | 3584 .. 3346 | 3576.4487 .. 61.47841 | 13490 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.207346031803593 | 0.2136292448885504 | 0.2104876383460717 | 0.21046124 .. 0.21046674 | 3222.9612 .. 3837.159 | 3504 .. 3466 | 3501.6152 .. -58.982677 | 13962 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.2136292448885504 | 0.21991245797350775 | 0.2167708514310291 | 0.21672955 .. 0.21671747 | 3282.833 .. 3728.5186 | 3748 .. 3770 | 3434.2856 .. 90.5686 | 15062 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
| 0.21991245797350775 | 0.2261956710584651 | 0.22305406451598642 | 0.22298157 .. 0.22308056 | 3189.86 .. 3806.1758 | 3702 .. 4002 | 3485.2192 .. 1.8451325 | 15688 | 0.0 .. 0.75 | 0.25 .. 1.0 | 0.125 .. 0.875 |
The meta field saves some information about how the power spectrum was calculated:
power.meta
{'Lbox': 1000.0,
'logk': False,
'paste': 'TSC',
'nmesh': 72,
'compensated': True,
'interlaced': True,
'poles': [0, 2, 4],
'nthread': 24,
'N_pos': 421791,
'is_weighted': False,
'field_dtype': numpy.float32,
'squeeze_mu_axis': True}
Compare with nbodykit#
Load presaved nbodykit computation:
comp_str = "_compensated" if compensated else ""
int_str = "_interlaced" if interlaced else ""
fn = f"../../../tests/data_power/nbody_{paste}{comp_str}{int_str}.npz"
data = np.load(fn)
k_nbody = data['k']
Pkmu_nbody = data['power'].real
Pell_nbody = data['power_ell'].real
Plot and compare:
colors = ['k', 'c', 'm', 'y']
plt.figure(figsize=(9, 7))
for i in range(nbins_mu):
if i == 0:
label1 = 'nbodykit'
label2 = 'abacus_power'
else:
label1 = label2 = None
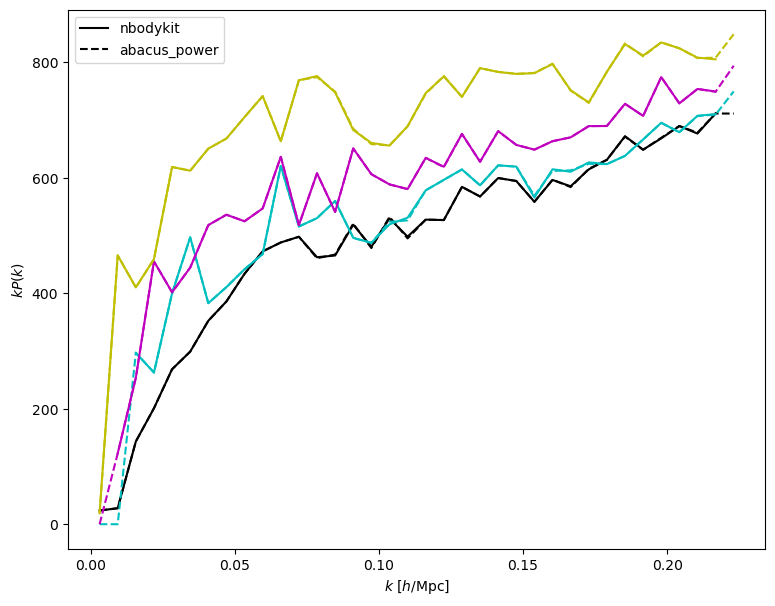
plt.plot(k_nbody, Pkmu_nbody[:, i] * k_nbody, c=colors[i], label=label1)
plt.plot(power['k_mid'], power['power'][:, i] * power['k_mid'], c=colors[i], ls='--', label=label2)
plt.ylabel(r"$k P(k)$")
plt.xlabel(r"$k \ [h/{\rm Mpc}]$")
plt.legend();
# plot and compare
plt.figure(figsize=(9, 7))
for i in range(len(poles)):
if i == 0:
label1 = 'nbodykit'
label2 = 'abacus_power'
else:
label1 = label2 = None
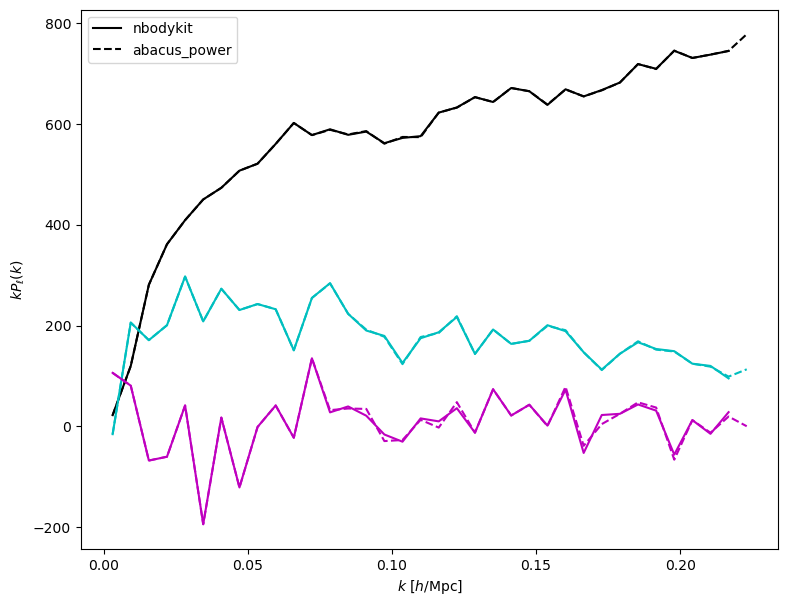
plt.plot(k_nbody, Pell_nbody[i, :] * k_nbody, c=colors[i], label=label1)
plt.plot(power['k_mid'], power['poles'][:,i] * power['k_mid'], c=colors[i], ls='--', label=label2)
plt.ylabel(r"$k P_\ell(k)$")
plt.xlabel(r"$k \ [h/{\rm Mpc}]$")
plt.legend();